A brief introduction to Derivative Calculus: Definition, History, and Rules

A brief introduction to Derivative Calculus: Definition, History, and Rules

Please kindly Share this Article on WhatsApp, Facebook and other Social Media Platform Using the Button Below. Thanks For Sharing🙏

In mathematics, finding the instantaneous rate of variation in a function based on specified factors is known as the derivative procedure. In Calculus, a derivative is a fundamental concept.

In simpler terms, a derivative is a contract between two parties that specifies the conditions under which payments are to be made between them based on the performance of an underlying asset.

The value of a derivative is based on the price of the underlying asset, and it can be bought and sold just like any other financial instrument. When we find the derivative the integration is the opposite.

In this article, we will discuss the definition of the derivative, notation of the derivative, meaning, and history of the derivative, rules of the derivative, and also an example of a derivative will be discussed.

Table of Contents

Definition of Derivative Calculus

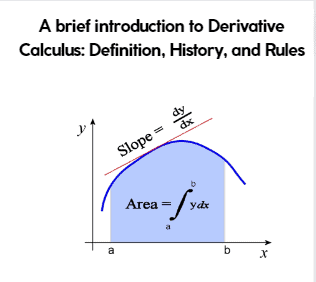
In calculus, the derivative is a fundamental concept of mathematics that denotes the rate of change of a function to its input value. It is a measure of how much a function changes as its input changes.

Formally, the limit of a ratio of a change in the function’s value to the change in the value of the input variable as the variation in the input variable near zero is described as the derivative of a function f(x) at a location x:

f'(x) = lim _{(Δx → 0)} [f (x + Δx) – f(x)] / Δx

It has many practical applications in science, engineering, economics, and other fields, such as finding the maximum and minimum values of a function, determining the velocity and acceleration of an object, and solving optimization problems.

Derivative notation:

Notation of derivative of a given function f(x), w.r.t to x is:

f'(x) (read as “f prime of x”)

Similarly, Leibniz’s notation is as follows:

dy/dx = f'(x) (read as “dee y by dee x equals f prime of x”)

These two notations denote the rate of change of a given function.

Meaning of derivative:

In calculus, the derivative is a mathematical concept that represents the rate at which a function changes w.r.t its input variable. It is a fundamental concept that allows us to analyze and understand the behavior of functions in a precise way.

The derivative gives us information about how the function is changing at a particular point, such as the slope of the tangent line to the function at that point. It also allows us to find the minimum and maximum values of a given function, define where the function is increasing or decreasing, and analyze the behavior of the function near critical points.

In calculus, a derivative is a fundamental tool that is used in many areas of mathematics, science, and engineering, including optimization, physics, economics, and more.

History of derivative

The concept of a derivative, which is a measure of how much one quantity changes to another quantity, can be traced back to the ancient Greeks. For example, Archimedes used the idea of a tangent line to find the slope of a curve at a given point.

However, the modern development of the derivative as a mathematical concept began in the 17th century with the work of Isaac Newton and Gottfried Wilhelm Leibniz.

Both mathematicians independently developed a way to calculate the rate of change of a function by considering the limit of the ratio of small changes in the function and the corresponding changes in the independent variable.

Today, derivatives continue to be a fundamental concept in mathematics and have applications in an inclusive range of fields, from economics and finance to engineering and nuclear physics.

Rules of Derivative Calculus

The fundamental rules of differentiation, are a collection of methods and techniques used to determine the derivative of a function that is also dependent on derivative rules.

Rules of function are given below:

Power rule:

If f(x) = x^n then f'(x) = n * x^(n-1). This rule applies to functions of form x raised to a power.

Product rule:

If f(x) = u(x) × v(x), then f'(x) = u'(x) × v(x) + u(x) × v'(x). To find the product of two functions this rule is applied.

Quotient rule:

If f(x) = u(x) / v(x), then f'(x) = [u'(x) × v(x) – u(x) × v'(x)] / v(x)^2. This rule applies to functions that are the quotient of two other functions.

Chain rule:

If f(x) = g(h(x)), then f'(x) = g'(h(x)) × h'(x). This rule applies to composite functions, where one function is applied to the output of another function.

These rules can be combined and applied to more complex functions through repeated application and simplification.

Notes on derivative:

The pace at which one variable changes to another is called a function’s derivative.
Using the first principle of differentiation, the derivative of any continuous function that can be differentiated on the range [a, b] is obtained.
Although their inverse can sometimes not be continuous, all derivative functions are continuous.
Derivatives can be used for hedging, but their use requires a sophisticated understanding of financial markets and instruments.

Solved Example of Derivative Calculus

Example.1:

Find the derivative of f(x) = 4x³ – 3x + 1 w.r.t x.

Solution:

Given: f(x) = 4x³ – 3x + 1

Step 1:

Take derivative on both the sides w.r.t x, we get;

f'(x) = d/dx [4x³ – 3x + 1]

= 4d/dx(x³) – 3d/dx(x) + d/dx (1)

Step 2:

Now simplify,

= 4 (3x²) – 3 (1) + (0

=12x²– 3

You can also use a derivative calculator to find the derivative of the function to get rid of complex calculus calculations.

Frequently Asked Question

Question no.1:

What is a derivative?

Answer:

In mathematics, a derivative tells how much change the behavior of a function when we put input value. It is the sudden rate of change of a function at a given point.

Question no.2:

What are the practical uses for derivatives?

Answer:

Derivatives have many practical applications, such as in calculating rates of change in physics and engineering problems, optimizing financial portfolios in economics, and modeling changes in populations or ecosystems in biology.

Question no.3:

Write down the way how we calculate the derivative of any function.

Answer:

There are several methods for finding the derivative of a function, but the most common method is to use the rules of differentiation. These rules allow you to find the derivative of a function based on its algebraic form.

Summary

In this article, we have discussed the definition of the derivative, notation of the derivative, meaning, history of the derivative, and rules of the derivative and also with the help of an example, the topic will be explained. After studying this article one can defend this topic easily.

A brief introduction to Derivative Calculus: Definition, History, and Rules

Definition of Derivative Calculus

Derivative notation:

Meaning of derivative:

History of derivative

Rules of Derivative Calculus

Notes on derivative:

Solved Example of Derivative Calculus

Frequently Asked Question

Summary

Recommended Post: